To assess the fundamental efficiency of a vehicle, it makes sense to compare the ‘total energy consumed’ with the momentum obtained (speed times weight). Clear back in 1950, Gabrielli and von Karman published “What Price Speed?”, a sweeping look at this topic for various forms of transportation.
Unfortunately, what it revealed is still true: the economics of flight are only reasonable when we fly big, heavy airplanes very, very fast… or when we fly very slowly with lots of wingspan. Airplanes in the middle miss the achievable efficiency target… by a factor of six!
To ask why until real answers emerge is to discover one of the largest opportunities in the modern world.
Two reasons especially stand out. One, airframe drag under power has always been assumed to be essentially the same or higher than the drag when towed or gliding. That isn’t true, nor should it be. A source of power can be used to cut drag by huge amounts, especially in the largely unexplored domain in question, if used to promote free circulation.
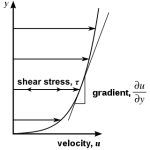
This can be illustrated, first by understanding there actually is a ‘static condition’ implicitly assumed in the math of lift and drag. It essentially says that if one drags a streamlined hull down a canal with a team of horses, the ‘horsepower’ it takes at a certain speed can be measured in the rope tension.
However, long ago it was learned that if one puts a motor of roughly half that horsepower on board, with proper propulsive design it can essentially achieve the same speed. Boat and aircraft propulsion is acting, not upon a fixed, immovable earth, but upon the fluid medium directly, which can be naturally circulated in a way that recovers much of the initial resistance. This is one reason why there are no tractor-prop submarines.
Second, the basic equations of drag and lift used for prediction embed this fixed, static assumption, rather than a dynamic circulation, which can only be directly computed upon a completed design.
It turns out that this assumption in the simplified math doesn’t approximate the physics of airflow in the unconstrained atmosphere equally in every domain, which can be seen by the changing coefficients required to make it work out at different speeds. Yet virtually every tool available early in the design process, or to a casual reviewer, relies entirely upon these representative equations.
The track record of GA inefficiency makes it obvious that something deeply hidden must be wrong in standard aeronautical practice. The above gives many clues about what it is.
In fact, a different aspect of this same topic once held center stage in the debate between ‘mathematically certain’ Cambridge physicists and technically competent German engineers. It took decades for Britain to catch on and accede to the obvious experimental results of Germany’s mastery of the circulation theory of lift. Now it is time for the circulation theory of drag reduction to be similarly advanced.
For the practical needs of aircraft designers, at the beginning of the 20th century Ludwig Prandtl and his student Blasius resolved d’ Alembert’s lossless fluid circulation paradox, a mystery that had been central to the puzzle of drag for close to two centuries, by postulating a physical basis for a mathematically required assumption. Their work gave us the ironically named ‘dynamic pressure’ concept; the ‘1/2 density times velocity squared’ portion of the basic lift and drag equation.
The irony of this postulate is that the required condition to allow our cavalier acceptance of this version of the standard ‘kinetic energy equation’ …is that there is…there MUST be…a non-dynamic, ‘static condition’ in the system somewhere, wherein air molecule movement is simply not allowed.
Since for a gas that’s not even remotely true, our use of the dynamic pressure equation depends upon a falsehood. This equation is used early, and pervades throughout aeronautics. It has preemptively cut off half of the experimentally demonstrated potential for drag reduction by labeling such results as anomalies and fictions.
What can be said now, as the true physics of circulation are finally reapplied to the topic of drag, is that the static condition assumption is only approximately useful for the flow regimes where either viscosity or inertia have the upper hand. In those ‘fast’ or ‘slow’ domains, this non-physical assumption holds reasonably enough, and consequently in those domains we’ve done quite well.
In the flight regime in question, though, actual boundary layer behaviors differ, sometimes dramatically, from the assumptions of this century-old mathematical model.
Even today this fact has remained largely invisible, although experimenters found it strongly implied for at least half that time. The modern version of the debate considers the merit of a host of turbulence models for CFD codes, each having improved accuracy in a particular domain, yet each conflicting and artificial.
It should therefore not be surprising that the natural application of circulation to drag reduction, using power, has been a sometimes controversial and always very poorly-understood topic. For example, the result shown here is ‘news’ known to some although applied successfully for forty years.
Today, the basic architecture of most aircraft reflects the pervasive influence of these underlying 2-D mathematical assumptions from a century ago, rather than the proper 4-D, dynamic physics. In fairness, it was until recently impossible to analyze such behaviors accurately, even though many designers have displayed a gift for its governing principles.
Nevertheless, the conventional aircraft architecture is fundamentally at odds with circulation methods of drag reduction, and therefore existing aircraft hardly benefit from concepts that require the body length and fineness ratio to be appropriate for the Reynolds number involved. Synergy uniquely resolves these issues in a transformative manner.
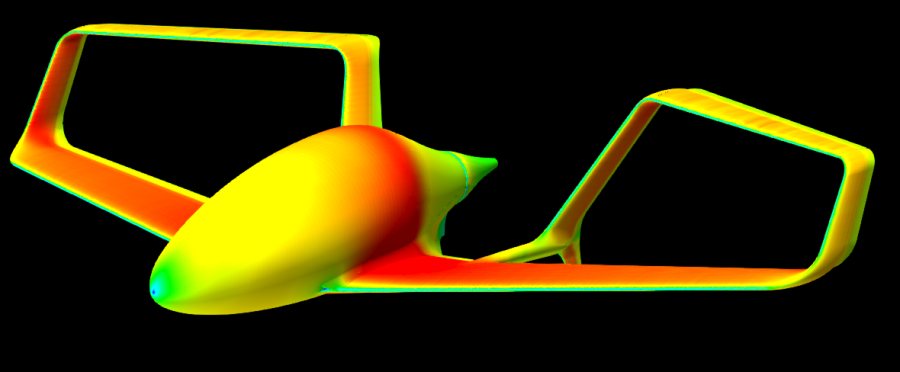
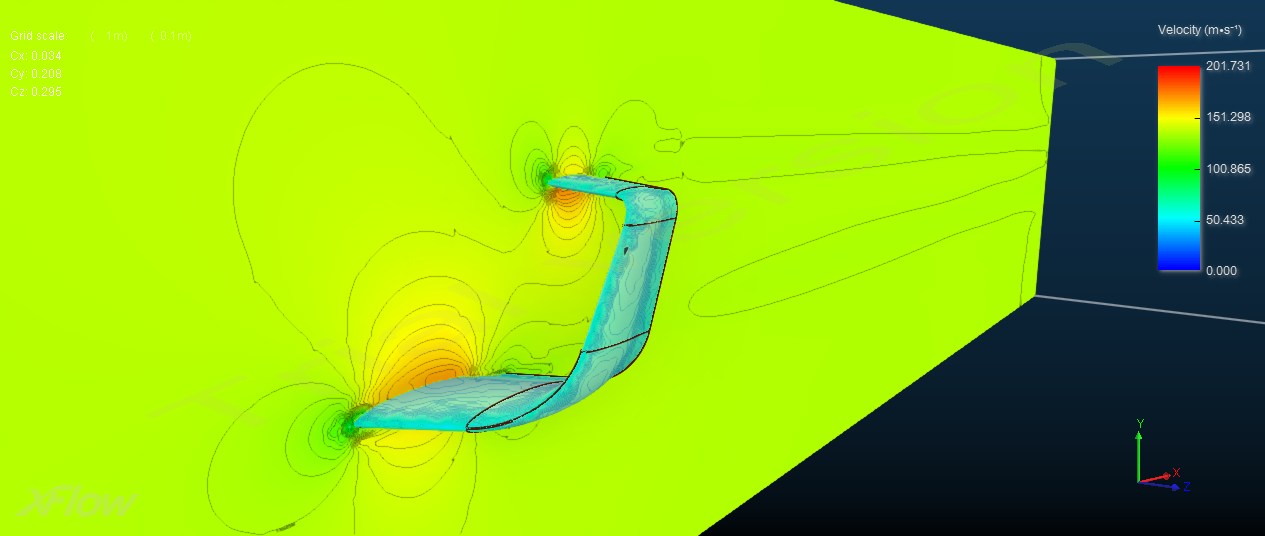
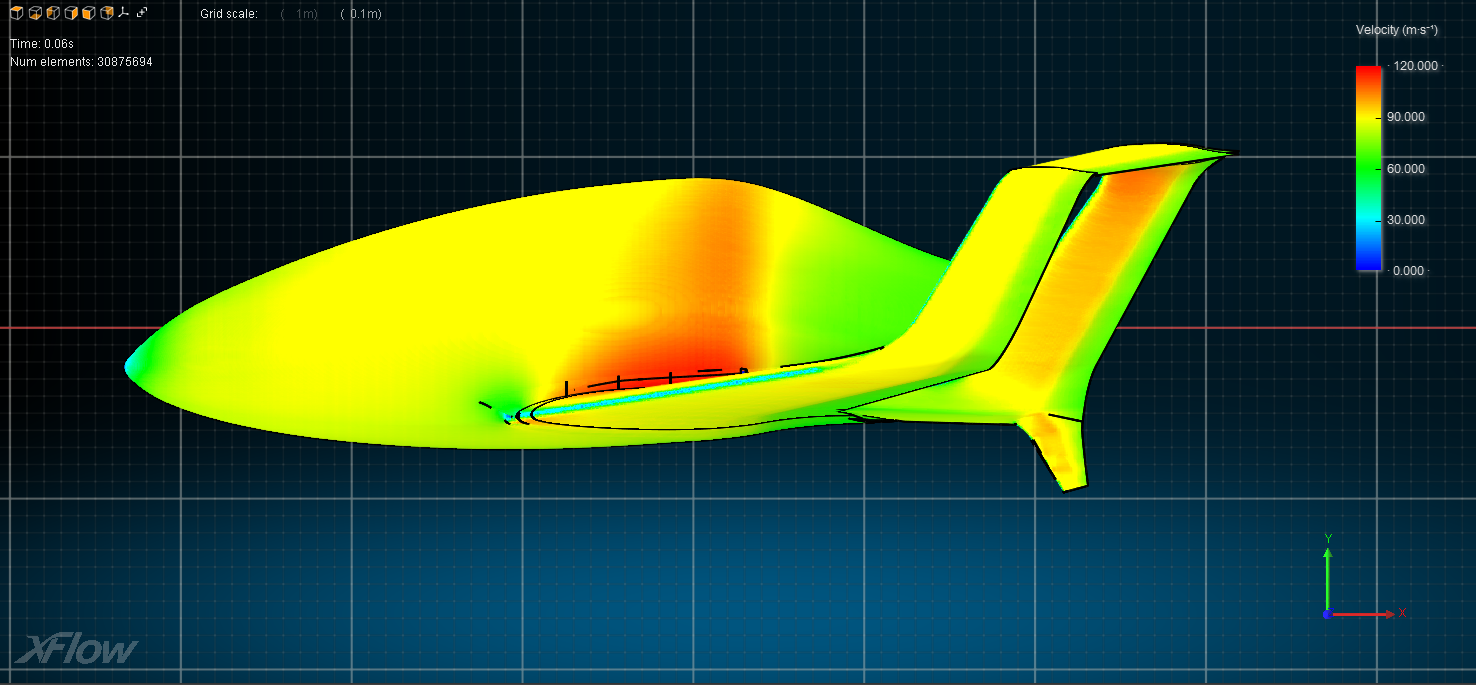
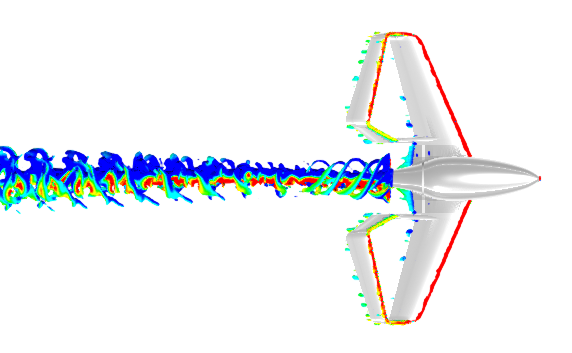
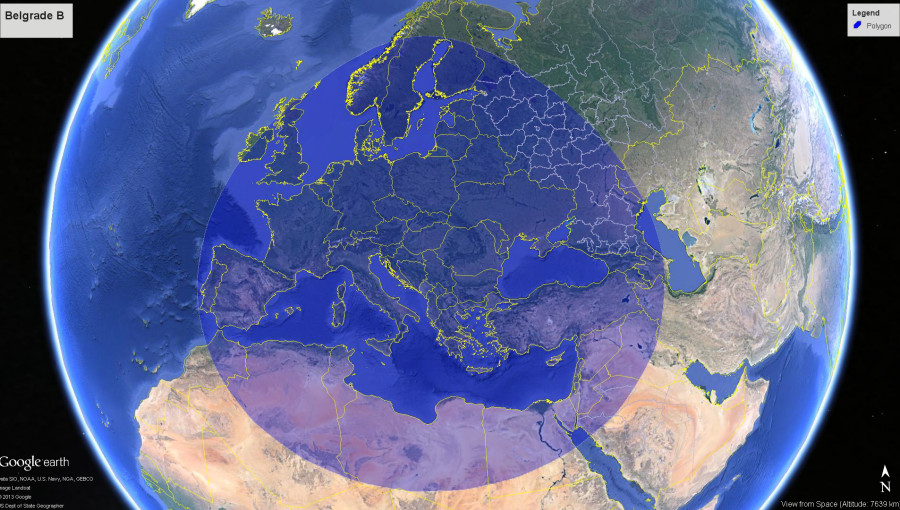
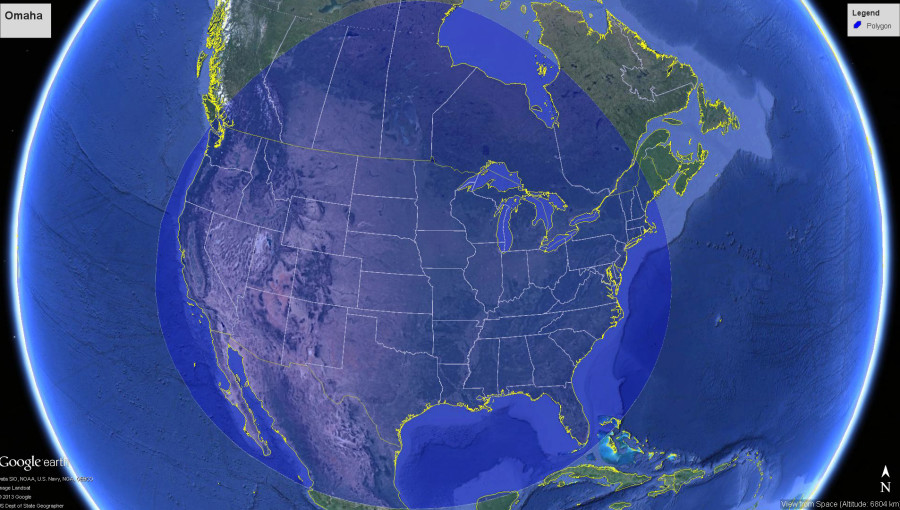
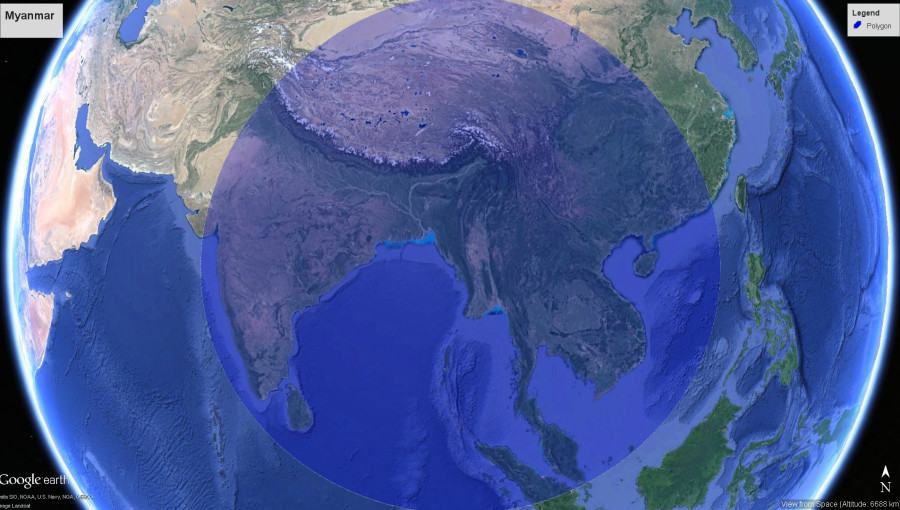
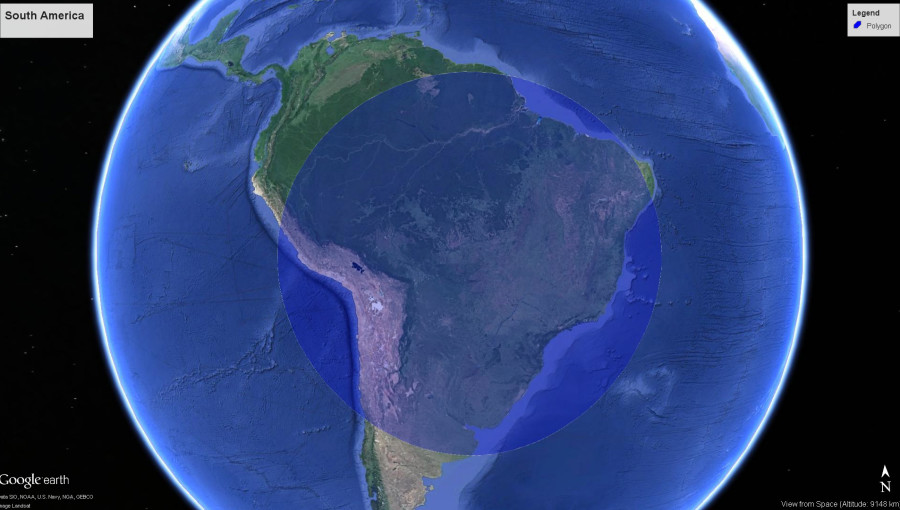
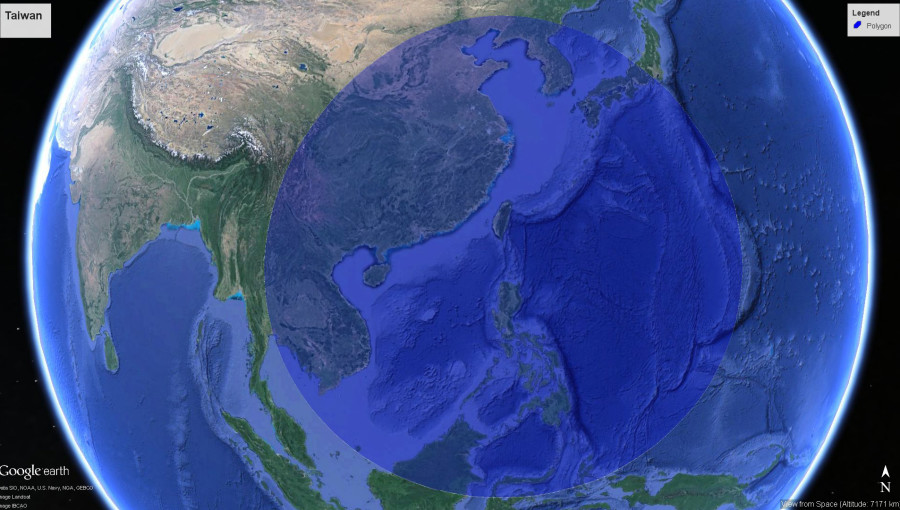
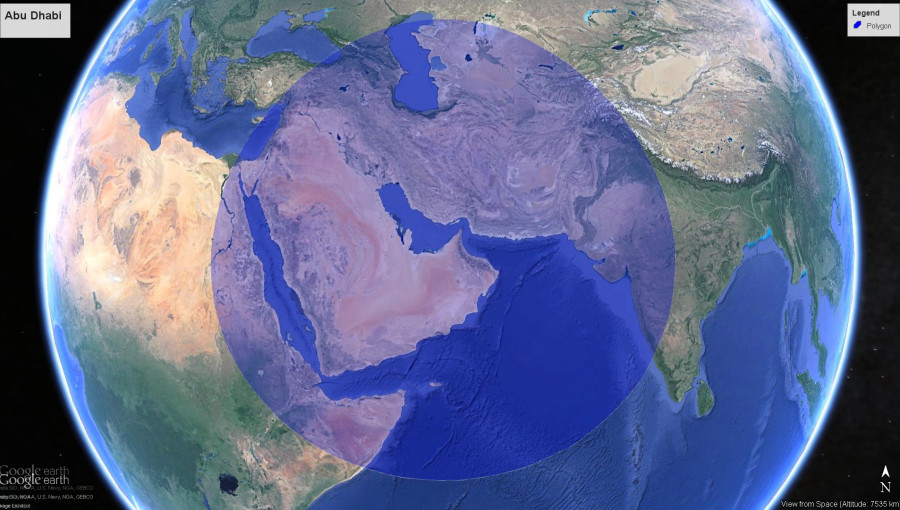
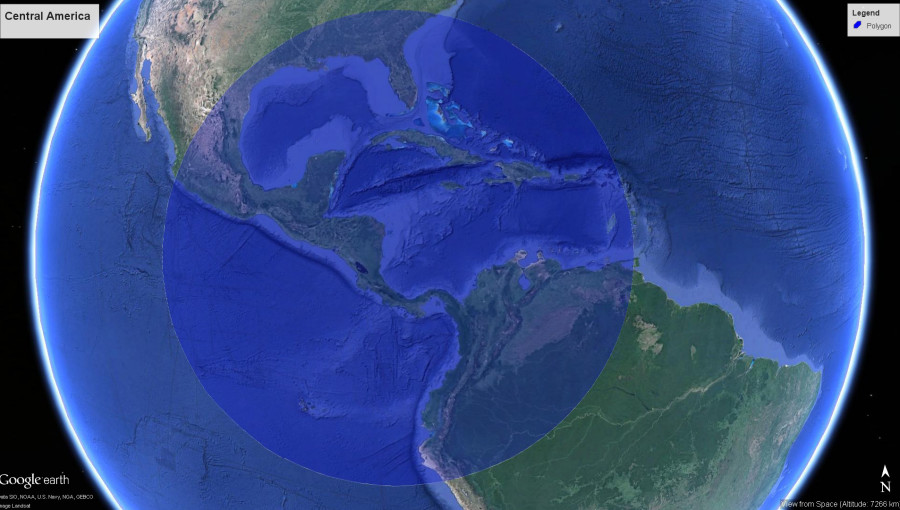
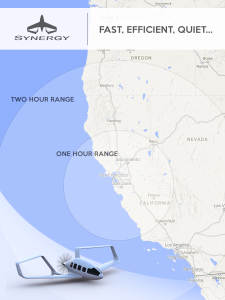Demand Aviation utterly changes everything: In Synergy, the same hour wasted on your Silicon Valley traffic jam would allow your commute to originate from South Lake Tahoe… or Santa Barbara, Santa Rosa, Reno, Monterrey, San Luis Obispo, Carson City…or anywhere in the entire central valley from Bakersfield to Sacramento to Redding. Draw the size of circle you want, around the place you need to be, and it will show you where you could live and how you could travel someday.
